영상의 기하학적 변환

영상의 기하학적 변환(Geometric transformation)
이동 변환(Translation trnaform)
전단 변환(Shear transform)
크기 변환(Scale transform)
1. 순방향 맵핑(Forward mapping)
2. 역방향 맵핑(Backward mapping)
보간법
1. resize() 함수를 이용한 사이즈 변환
2. 영상 데이터 축소 시 주의할 점
회전 변환(Rotation transform)
기하학적 변환
어파인 변환(Affine transform)
투시 변환(Perspective tranform)
리맵핑(Remapping)

영상의 기하학적 변환(Geometric transformation)

영상을 구선하는 픽셀의 구조를 변경함으로써 전체 영상의 모양을 바꾸는 작업이다. 전처리, 영상 접합, 왜곡 제거 등이 이에 해당한다.

영상의 변환 방법은 크게 두 가지로 나눠진다. 첫 번째로 원본 영상의 직선 형태를 변환 후에도 직선으로 유지하는 형태의 변환이다. 두 번째는 원본 영상의 직선 형태를 곡선 형태로 변환하는 혹은 그 반대인 변환 방법들이 존재한다.

이동 변환(Translation trnaform)

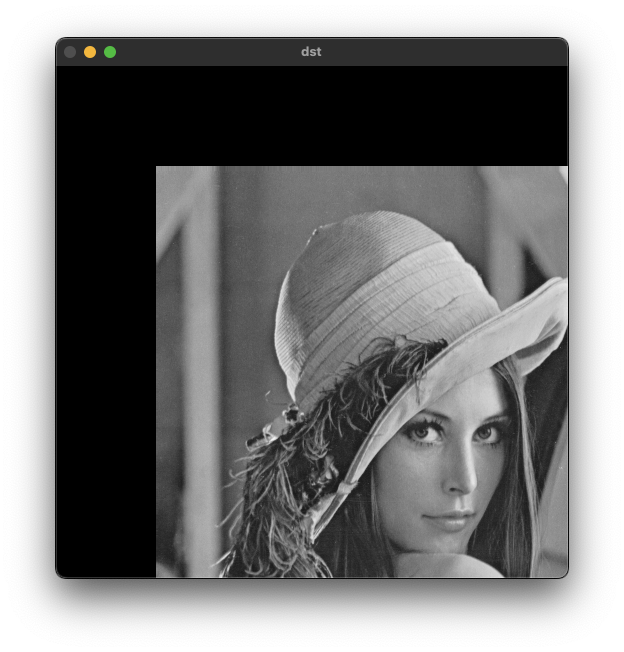
이동 변환은 영상의 가로 또는 세로 방향으로 영상을 특정 크기만큼 이동시키는 변환 방법이다.

좌표를 이용하여 식으로 표현하면 다음과 같다. \(\begin{cases} x`=x+a\\ y`=y+b \end{cases} \\\)

원점이 (0,0)에서 (a,b)로 이동했기 때문에 영상 전체의 픽셀이 마찬가지로 원래 위치에서 (a, b)만큼 증가하는 형태가 되어야 한다.

\(\begin{bmatrix} x`\\ y` \end{bmatrix} =\begin{bmatrix} 1 & 0\\ 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix} +\begin{bmatrix} a\\ b \end{bmatrix} \\\) 위와 같이 행렬로 표현이 가능하며 \(\begin{bmatrix} x`\\ y` \end{bmatrix} =\begin{bmatrix} 1 & 0 & a\\ 0 & 1 & b \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}\) 행렬 연산 과정에서 덧셈이 포함되는 경우 식의 전개가 복잡해진다. 때문에 위 식처럼 덧셈 부분을 업애기 위해 곱셈 부분에 하나의 차원을 늘릴 수 있다. 이러한 좌표계를 동차좌표계(Homogeneous Coordinate)라고 한다.

void ex_translate(){
    Mat src = imread("../data/lenna.bmp", IMREAD_GRAYSCALE);

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}

	Mat dst = Mat::zeros(src.size(), CV_8UC1);

	for (int y = 0; y < src.rows; y++) {
		for (int x = 0; x < src.cols; x++) {
			int x_ = x + 100;
			int y_ = y + 100;
			if (x_ < 0 || x_ >= dst.cols) continue;
			if (y_ < 0 || y_ >= dst.rows) continue;
			dst.at<uchar>(y_, x_) = src.at<uchar>(y, x);
		}
	}
	imshow("src", src);
	imshow("dst", dst);
	waitKey();

}

void ex_processing(){
    Mat src = imread("../data/lenna.bmp", IMREAD_GRAYSCALE);

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}
	float data[] = {1, 0, 100, 0, 1, 100};
	Mat affine = Mat(2,3, CV_32FC1, data);
	// or
	// Mat affine = (Mat_<float>(2, 3) << 1, 0, 100, 0, 1, 100);

	Mat dst;
	warpAffine(src, dst, affine, Size());


	imshow("src", src);
	imshow("dst", dst);
	waitKey();

}

전단 변환(Shear transform)

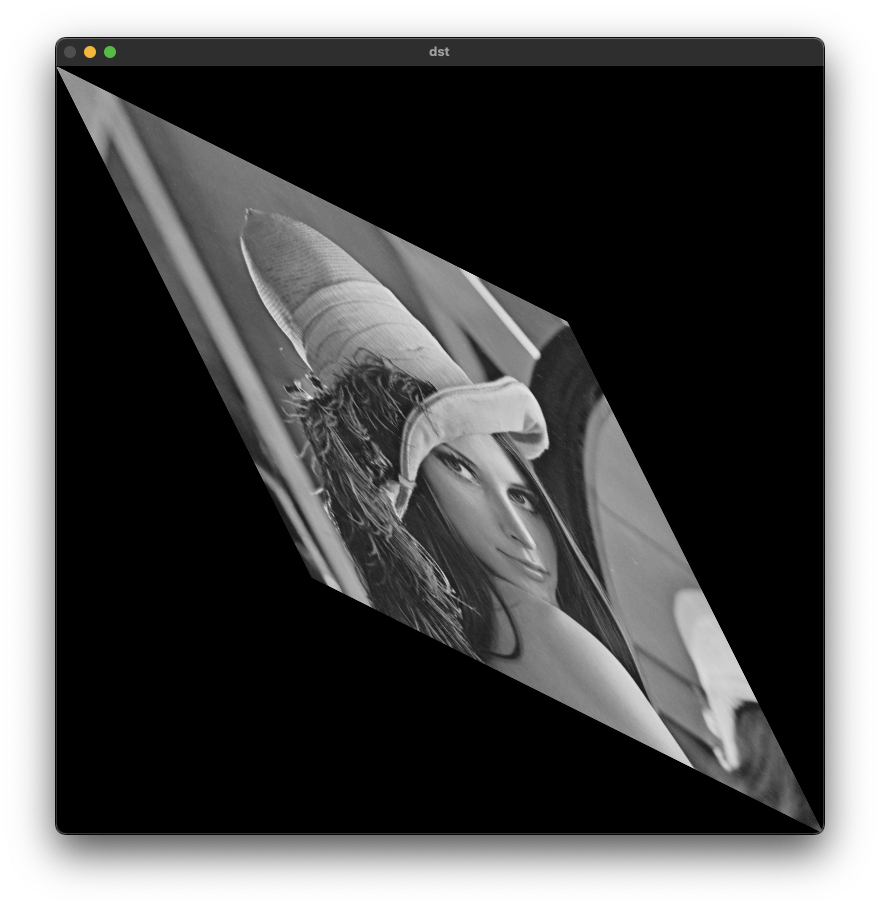
층밀림 변환이라고 하며, 직사각형 형태의 영상 데이터를 한쪽 방햫 혹은 양쪽 방향을 밀어서 평행사변형 모양으로 변환하는 방법이다.

\[\begin{bmatrix} x`\\ y` \end{bmatrix} =\begin{bmatrix} 1 & m_{y} & 0\\ m_{x} & 1 & 0 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}\]

void ex_processing(){
    Mat src = imread("../data/lenna.bmp", IMREAD_GRAYSCALE);

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}
    
	Mat dst(src.rows * 3 / 2, src.cols, src.type(), Scalar(0));

	double m = 0.5;
	for (int y = 0; y < src.rows; y++) {
		for (int x = 0; x < src.cols; x++) {
			int nx = x;
			int ny = int(y + m*x);
			dst.at<uchar>(ny, nx) = src.at<uchar>(y, x);
		}
	}

	imshow("src", src);
	imshow("dst", dst);

	waitKey();

}

void ex_processing(){
    Mat src = imread("../data/lenna.bmp", IMREAD_GRAYSCALE);

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}
	float data[] = {1, 0.5, 0, 0, 1, 0};
	Mat affine = Mat(2,3, CV_32FC1, data);
	// or
	// Mat affine = (Mat_<float>(2, 3) << 1, 0.5, 0, 0, 1, 0);

	Mat dst;
	warpAffine(src, dst, affine, Size(src.cols * 3 / 2, src.rows));

	imshow("src", src);
	imshow("dst", dst);

	waitKey();

}

void ex_processing(){
    Mat src = imread("../data/lenna.bmp", IMREAD_GRAYSCALE);

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}
    
	float data[] = {1, 0.5, 0,
                    0.5, 1, 0};
	Mat affine = Mat(2,3, CV_32FC1, data);

	Mat dst;
	warpAffine(src, dst, affine, Size(src.cols * 1.5, src.rows * 1.5));

s
	imshow("src", src);
	imshow("dst", dst);

	waitKey();

}

크기 변환(Scale transform)

영상의 크기를 변환하는 방법이다. 스케일 비율에 따라 크기를 조절한다.

\[\begin{bmatrix} x`\\ y` \end{bmatrix} =\begin{bmatrix} s_{x} & 0 & 0\\ 0 & s_{y} & 0 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}\]

순방향 맵핑(Forward mapping)

for loop를 이용한 이미지 확대 방법을 이용해서 영상의 크기를 2배 확대하는 경우 빈 공간이 생기는것을 확인할 수 있다. 입력 영상의 좌표를 2배하여 출력 영상의 값으로 사용하기 때문이다.

\[\begin{cases} x`=s_{x} x\\ y`=s_{y} y \end{cases}\]

void ex_processing(){
    Mat src = imread("../data/lenna.bmp", IMREAD_GRAYSCALE);

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}
    
	Mat dst = Mat::zeros(src.rows * 2, src.cols * 2, CV_8UC1);

	for (int y = 0; y < src.rows; y++) {
		for (int x = 0; x < src.cols; x++) {
			int x_ = x * 2;
			int y_ = y * 2;

			dst.at<uchar>(y_, x_) = src.at<uchar>(y, x);
		}
	}

	imshow("src", src);
	imshow("dst", dst);
	waitKey();

}

역방향 맵핑(Backward mapping)

역방향 맵핑을 통해 순방향 맵핑에서 나타나는 문제를 해결할 수 있다. 출력 영상의 좌표를 기준으로 스케일 팩터(s)를 나눈 원본 영상의 위치의 픽셀값을 가져온다. 하지만 역방향 맵핑의 경우 원본 영상에서 중복된 픽셀을 가져오기 때문에 계산 현상이 심한것을 확인할 수 있다.

\[\begin{cases} x= x`/s_{x}\\ y=y`/s_{y} \end{cases}\]

void ex_processing(){
    Mat src = imread("../data/camera.bmp", IMREAD_GRAYSCALE);

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}
    
	Mat dst = Mat::zeros(src.rows * 2, src.cols * 2, src.type());

	for (int y_ = 0; y_ < dst.rows; y_++) {
		for (int x_ = 0; x_ < dst.cols; x_++) {
			int x = x_ / 2;
			int y = y_ / 2;
			dst.at<uchar>(y_, x_) = src.at<uchar>(y, x);
		}
	}

	imshow("src", src);
	imshow("dst", dst);
	waitKey();
}

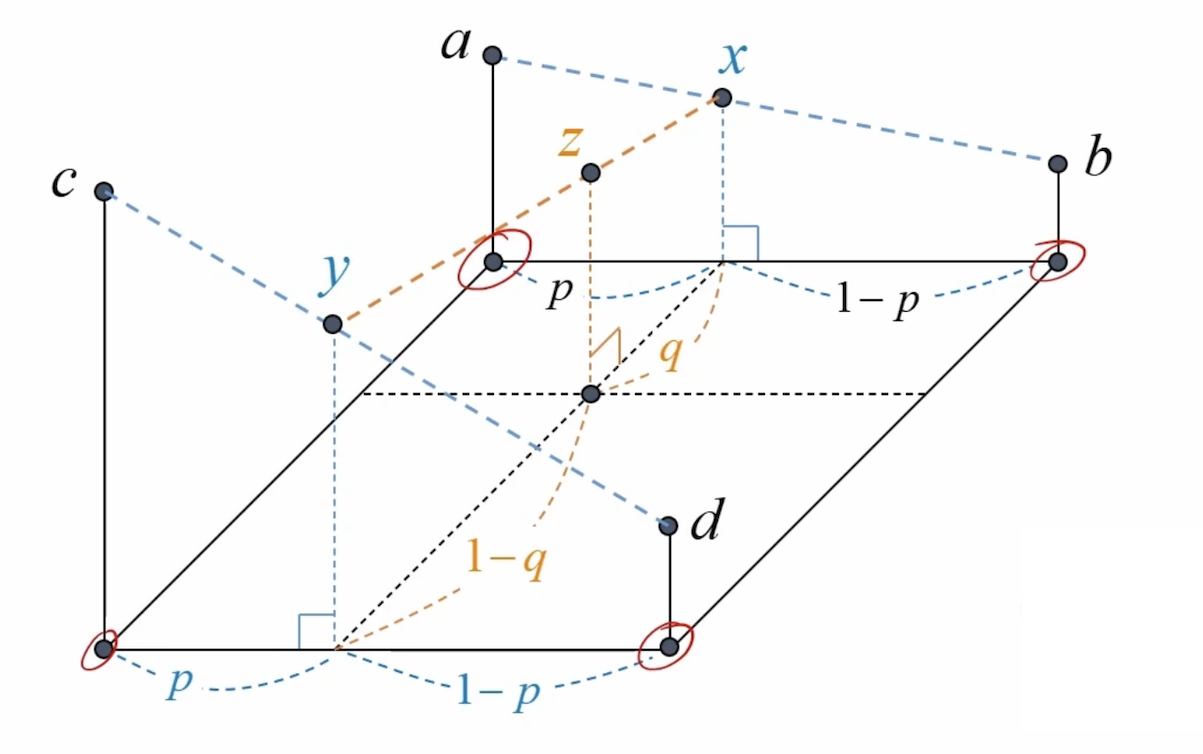
보간법

\(\begin{align*} x & =( 1-p) a+pb\\ y & =( 1-p) d+pc\\ z & =( 1-p) y+px\\ z & = ( 1-q)[( 1-p) d+pc] +q[( 1-p) a+pb]\\ & = ( 1-p)( 1-q) d+( 1-q) pc+( 1-p) qa+pqb \end{align*}\)

void resizeBilinear(const Mat& src, Mat& dst, Size size)
{
	dst.create(size.height, size.width, CV_8U);

	int x1, y1, x2, y2;	double rx, ry, p, q, value;
	double sx = static_cast<double>(src.cols - 1) / (dst.cols - 1);
	double sy = static_cast<double>(src.rows - 1) / (dst.rows - 1);

	for (int y = 0; y < dst.rows; y++) {
		for (int x = 0; x < dst.cols; x++) {
			rx = sx * x;			ry = sy * y;
			x1 = cvFloor(rx);		y1 = cvFloor(ry);
			x2 = x1 + 1; if (x2 == src.cols) x2 = src.cols - 1;
			y2 = y1 + 1; if (y2 == src.rows) y2 = src.rows - 1;
			p = rx - x1;			q = ry - y1;

			value = (1. - p) * (1. - q) * src.at<uchar>(y1, x1)
				+ p * (1. - q) * src.at<uchar>(y1, x2)
				+ (1. - p) * q * src.at<uchar>(y2, x1)
				+ p * q * src.at<uchar>(y2, x2);

			dst.at<uchar>(y, x) = static_cast<uchar>(value + .5);
		}
	}
}

    Mat src = imread("../data/camera.bmp", IMREAD_GRAYSCALE);

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}
    
	Mat dst;
	resizeBilinear(src, dst, Size(1200, 1200));

	imshow("src", src);
	imshow("dst", dst);
	waitKey();

resize() 함수를 이용한 사이즈 변환

void ex_processing(){
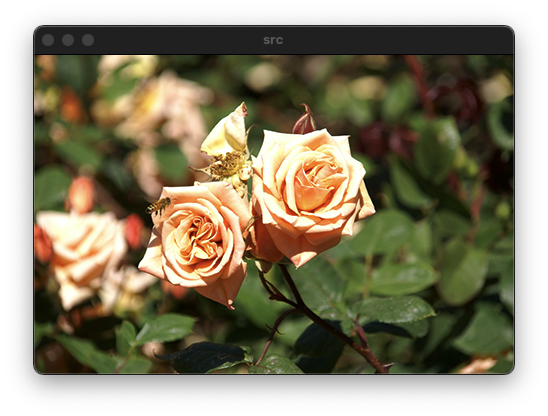
    Mat src = imread("../data/rose.bmp");

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}
    
	Mat dst1, dst2, dst3, dst4;
	resize(src, dst1, Size(), 4, 4, INTER_NEAREST);
	resize(src, dst2, Size(1920, 1280));
	resize(src, dst3, Size(1920, 1280), 0, 0, INTER_CUBIC);
	resize(src, dst4, Size(1920, 1280), 0, 0, INTER_LANCZOS4);

	imshow("src", src);
	imshow("dst1", dst1(Rect(400, 500, 400, 400)));
	imshow("dst2", dst2(Rect(400, 500, 400, 400)));
	imshow("dst3", dst3(Rect(400, 500, 400, 400)));
	imshow("dst4", dst4(Rect(400, 500, 400, 400)));
	waitKey();

}

영상 데이터 축소 시 주의할 점

영상을 축소하는 것은 확대하는 것보다 단순하게 생각할 수 있지만 원본 영상을 급격하게 축소시키는 경우 열화 현상에 의해 화질이 나빠질 수 있다. 원본 영상에 blur 처리를 한 후 영상을 축소하거나, INTER_AREA 라는 옵션을 이용하면 된다.

회전 변환(Rotation transform)

영상을 특정 각도만큼 회전시키는 변환 방법이다. OpenCV에서는 기본적으로 반시계 방향을 정방향으로 정의한다.

정방향 맵핑(Forward mapping)

\(\begin{cases} x`=cos\theta \cdotp x +sin\theta \cdot y\\ y`=-sin\theta \cdot x+cos\theta \cdot y \end{cases}\)

\[\begin{bmatrix} x`\\ y` \end{bmatrix} =\begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix} +\begin{bmatrix} 0\\ 0 \end{bmatrix}\] \[\begin{bmatrix} x`\\ y` \end{bmatrix} =\begin{bmatrix} cos\theta & sin\theta & 0\\ -sin\theta & cos\theta & 0 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix}\]

역방향 맵핑(Backward mapping)

\(\begin{align*} \begin{bmatrix} x`\\ y` \end{bmatrix} & =\begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}\begin{bmatrix} x\\ y \end{bmatrix}\\ \begin{bmatrix} x\\ y \end{bmatrix} & =\begin{bmatrix} cos\theta & sin\theta \\ -sin\theta & cos\theta \end{bmatrix}^{-1}\begin{bmatrix} x`\\ y` \end{bmatrix}\\ & =\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \end{bmatrix}\begin{bmatrix} x`\\ y` \end{bmatrix} \end{align*}\)

getRotationMatrix2D() 함수

2x3 크기의 affine matrix를 생성하는 함수이다. center는 회전에 중심이 되는 원본 영상의 중점을 의미한다(e.g. src.cols/2.f, src/rosw/2.f). angle은 회전할 각도를 입력하며 degree를 기준으로 한다.

영상을 그대로 회전 변환하면 중심축이 좌측 상단이기 때문에 기준점을 중심으로 옮겨 주어야 한다.

\[\begin{align*} \begin{bmatrix} x`\\ y`\\ 1 \end{bmatrix} & =\begin{bmatrix} 1 & 0 & c_{x}\\ 0 & 1 & c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} \alpha & \beta & 0\\ -\beta & \alpha & 0\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & -c_{x}\\ 0 & 1 & -c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix} \ \begin{cases} \alpha =cos\theta \\ \beta =sin\theta \end{cases}\\ & =\begin{bmatrix} \alpha & \beta & c_{x}\\ -\beta & \alpha & c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} 1 & 0 & -c_{x}\\ 0 & 1 & -c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix} \ \\ & =\begin{bmatrix} \alpha & \beta & -\alpha c_{x} -\beta c_{y} +c_{x}\\ -\beta & \alpha & \beta c_{x} -\alpha c_{y} +c_{y}\\ 0 & 0 & 1 \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix} \ \end{align*}\]

center: 회전 중심 좌표
angle: 회전 각도(반시계 방향)
scale: 회전 후 확대 비율

Mat getRotationMatrix2D(Point2f center, double angle, double scale);

warpAffine() 함수

affine matrix를 원본 영상에 적용해서 반환하는 함수이다.

void warpAffine( InputArray src, OutputArray dst,
                              InputArray M, Size dsize,
                              int flags = INTER_LINEAR,
                              int borderMode = BORDER_CONSTANT,
                              const Scalar& borderValue = Scalar());

src: input image.
dst: output image that has the size dsize and the same type as src.
M: [2 x 3] transformation matrix. 
dsize: size of the output image.
flags: 보간법을 선택
//! interpolation algorithm
enum InterpolationFlags{
    /** nearest neighbor interpolation */
    INTER_NEAREST        = 0,
    /** bilinear interpolation */
    INTER_LINEAR         = 1,
    /** bicubic interpolation */
    INTER_CUBIC          = 2,
    /** resampling using pixel area relation. It may be a preferred method for image decimation, as
    it gives moire'-free results. But when the image is zoomed, it is similar to the INTER_NEAREST
    method. */
    INTER_AREA           = 3,
    /** Lanczos interpolation over 8x8 neighborhood */
    INTER_LANCZOS4       = 4,
    /** Bit exact bilinear interpolation */
    INTER_LINEAR_EXACT = 5,
    /** Bit exact nearest neighbor interpolation. This will produce same results as
    the nearest neighbor method in PIL, scikit-image or Matlab. */
    INTER_NEAREST_EXACT  = 6,
    /** mask for interpolation codes */
    INTER_MAX            = 7,
    /** flag, fills all of the destination image pixels. If some of them correspond to outliers in the
    source image, they are set to zero */
    WARP_FILL_OUTLIERS   = 8,
    /** flag, inverse transformation

    For example, #linearPolar or #logPolar transforms:
    - flag is __not__ set: \f$dst( \rho , \phi ) = src(x,y)\f$
    - flag is set: \f$dst(x,y) = src( \rho , \phi )\f$
    */
    WARP_INVERSE_MAP     = 16
};
borderMode: pixel extrapolation method (see #BorderTypes); when borderMode=#BORDER_TRANSPARENT, it means that the pixels in the destination image corresponding to the "outliers" in the source image are not modified by the function.
//! Various border types, image boundaries are denoted with `|`
//! @see borderInterpolate, copyMakeBorder
enum BorderTypes {
    BORDER_CONSTANT    = 0, //!< `iiiiii|abcdefgh|iiiiiii`  with some specified `i`
    BORDER_REPLICATE   = 1, //!< `aaaaaa|abcdefgh|hhhhhhh`
    BORDER_REFLECT     = 2, //!< `fedcba|abcdefgh|hgfedcb`
    BORDER_WRAP        = 3, //!< `cdefgh|abcdefgh|abcdefg`
    BORDER_REFLECT_101 = 4, //!< `gfedcb|abcdefgh|gfedcba`
    BORDER_TRANSPARENT = 5, //!< `uvwxyz|abcdefgh|ijklmno`

    BORDER_REFLECT101  = BORDER_REFLECT_101, //!< same as BORDER_REFLECT_101
    BORDER_DEFAULT     = BORDER_REFLECT_101, //!< same as BORDER_REFLECT_101
    BORDER_ISOLATED    = 16 //!< do not look outside of ROI
};
borderValue: value used in case of a constant border; by default, it is 0.

Example code

void on_rotate(int pos, void* data)
{
	Mat src = *(Mat*)data;

	float degree = (float)pos;
	Point2f pt(src.cols / 2.f, src.rows / 2.f);
	Mat rot = getRotationMatrix2D(pt, degree, 1.0);

	Mat dst;
	warpAffine(src, dst, rot, Size());

	imshow("dst", dst);
}

void ex_processing(){
    Mat src = imread("../data/rose.bmp");

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}
    
	imshow("src", src);

	namedWindow("dst");
	createTrackbar("angle", "dst", 0, 360, on_rotate, (void*)&src);
	on_rotate(0, (void*)&src);

	waitKey();

}

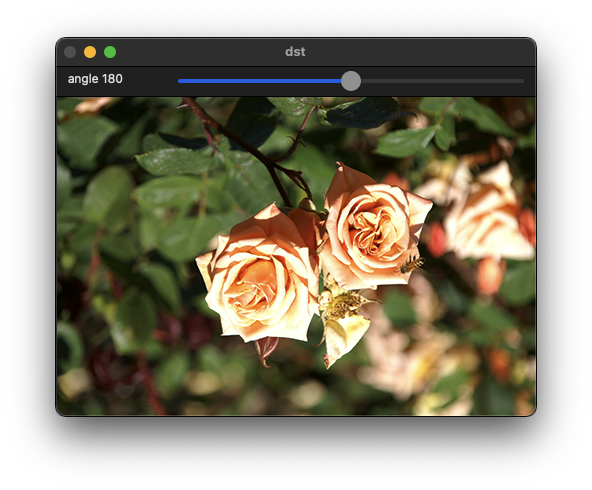
기하학적 변환

void flip(InputArray src, OutputArray dst, int flipCode);

src: input array.
dst: output array of the same size and type as src.
flipCode: a flag to specify how to flip the array; 0 means
flipping around the x-axis and positive value (for example, 1) means
flipping around y-axis. Negative value (for example, -1) means flipping around both axes.
1: 좌우 대칭
0: 상하 대칭
-1: 좌우 상하 대칭

void ex_processing(){
    Mat src = imread("../data/rose.bmp"), dst;

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}
    
    flip(src, dst, 1);

	imshow("src", src);
    imshow("dst", dst);
	waitKey();

}

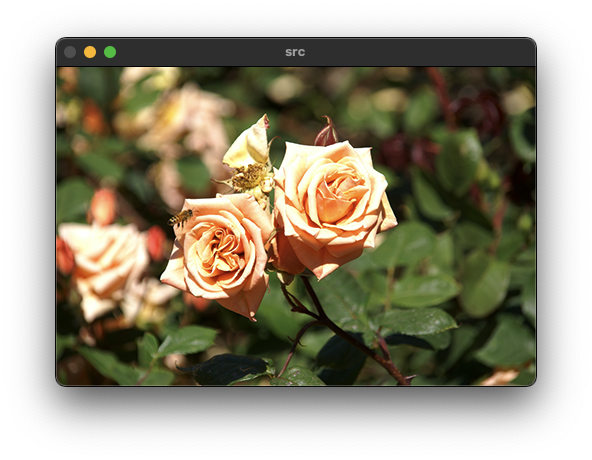
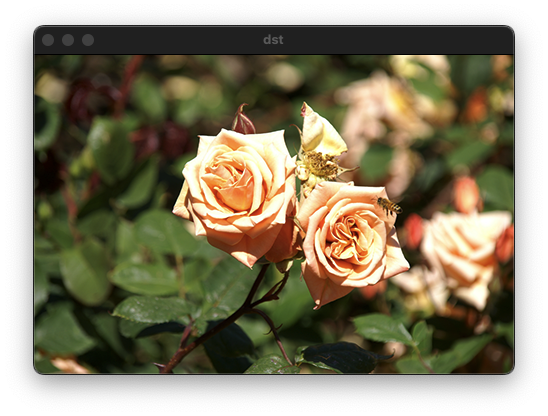
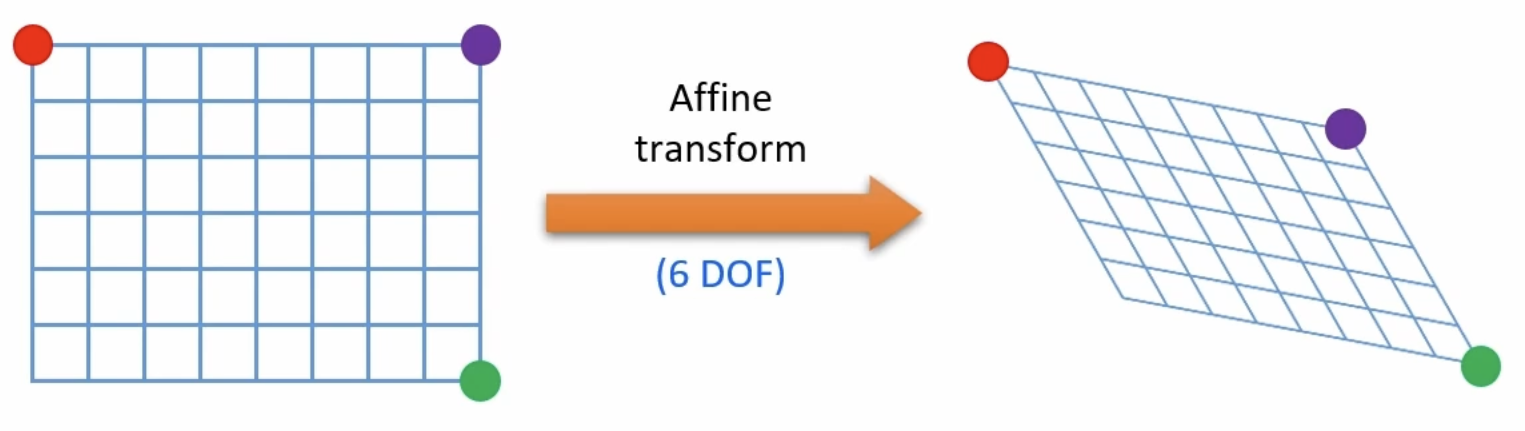
어파인 변환(Affine transform)

Affine transform 같은 경우 평행사변형 형태로 변환하기 때문에 3개의 점의 변환 정보만 알아도 나머지 1개는 3개의 점으로 구할 수 있다. 빨간색 점을 좌표 편면상의 한 점의 이동이라고 봤을 때, x와 y에 대한 두 식으로 표현이 가능하다. 나머지 두 점 또한 4개의 식으로 표현이 가능하기 때문에 총 6개의 식으로 위 변환을 정의할 수 있다.

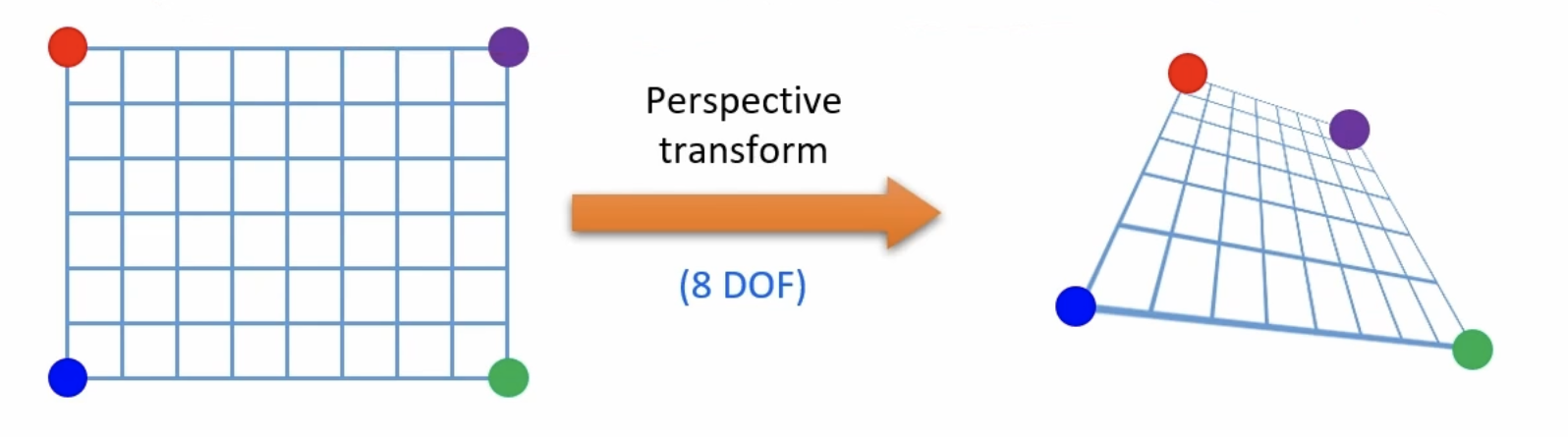
투시 변환(Perspective tranform)

Perspectiva transform은 8개의 방정식으로 정의가 가능하며, 이를 통한 affine matrix를 구할 수 있다.

\(\begin{aligned} \begin{bmatrix} wx`\\ wy`\\ w \end{bmatrix} & =\begin{bmatrix} a & b & c\\ d & e & f\\ g & h & i \end{bmatrix}\begin{bmatrix} x\\ y\\ 1 \end{bmatrix} \ \ \end{aligned}\) \(\begin{cases} x` & =\frac{ax+by+c}{gx+hy+i}\\ y` & =\frac{dx+ey+f}{gx+hy+i} \end{cases}\) \(\begin{cases} x` & =ax+by+c-gxx`-hx`y\\ y` & =dx+ey+f-gxy`-yy` \end{cases}\) \(\begin{cases} x_{1}^{`} & =ax_{1} +by_{1} +c & & -gx_{1} x_{1}^{`} -hx_{1} y_{1}^{`}\\ y_{1}^{`} & = & dx_{1} +ey_{1} +f & -gx_{1} y_{1}^{`} -hy_{1} y_{1}^{`} \end{cases}\) \(\begin{bmatrix} x_{1}^{`}\\ y_{1}^{`}\\ x_{2}^{`}\\ y_{2}^{`}\\ x_{3}^{`}\\ y_{3}^{`}\\ x_{4}^{`}\\ y_{4}^{`} \end{bmatrix} =\begin{bmatrix} x_{1} & y_{1} & 1 & 0 & 0 & 0 & -x_{1} x_{1}^{`} & -x_{1}^{`} y_{1}\\ 0 & 0 & 0 & x_{1} & y_{1} & 1 & -x_{1} y_{1}^{`} & -y_{1} y_{1}^{`}\\ x_{2} & y_{2} & 1 & 0 & 0 & 0 & -x_{2} x_{2}^{`} & -x_{2}^{`} y_{2}\\ 0 & 0 & 0 & x_{2} & y_{2} & 1 & -x_{2} y_{2}^{`} & -y_{2} y_{2}^{`}\\ x_{3} & y_{3} & 1 & 0 & 0 & 0 & -x_{3} x_{3}^{`} & -x_{3}^{`} y_{3}\\ 0 & 0 & 0 & x_{3} & y_{3} & 1 & -x_{3} y_{3}^{`} & -y_{3} y_{3}^{`}\\ x_{4} & y_{4} & 1 & 0 & 0 & 0 & -x_{4} x_{4}^{`} & -x_{4}^{`} y_{4}\\ 0 & 0 & 0 & x_{4} & y_{4} & 1 & -x_{4} y_{4}^{`} & -y_{4} y_{4}^{`} \end{bmatrix}\begin{bmatrix} a\\ b\\ c\\ d\\ e\\ f\\ g\\ h \end{bmatrix}\)

Mat getPerspectiveTransform(InputArray src, InputArray dst, int solveMethod = DECOMP_LU);

src: Coordinates of quadrangle vertices in the source image.
dst: Coordinates of the corresponding quadrangle vertices in the destination image.
solveMethod: method passed to cv::solve (#DecompTypes)

void warpPerspective( InputArray src, OutputArray dst,
                                   InputArray M, Size dsize,
                                   int flags = INTER_LINEAR,
                                   int borderMode = BORDER_CONSTANT,
                                   const Scalar& borderValue = Scalar());

src: input image.
dst: output image that has the size dsize and the same type as src .
M: \f$3\times 3\f$ transformation matrix.
dsize: size of the output image.
flags: combination of interpolation methods (#INTER_LINEAR or #INTER_NEAREST) and the
optional flag #WARP_INVERSE_MAP, that sets M as the inverse transformation (
\f$\texttt{dst}\rightarrow\texttt{src}\f$ ).
borderMode: pixel extrapolation method (#BORDER_CONSTANT or #BORDER_REPLICATE).
borderValue: value used in case of a constant border; by default, it equals 0.

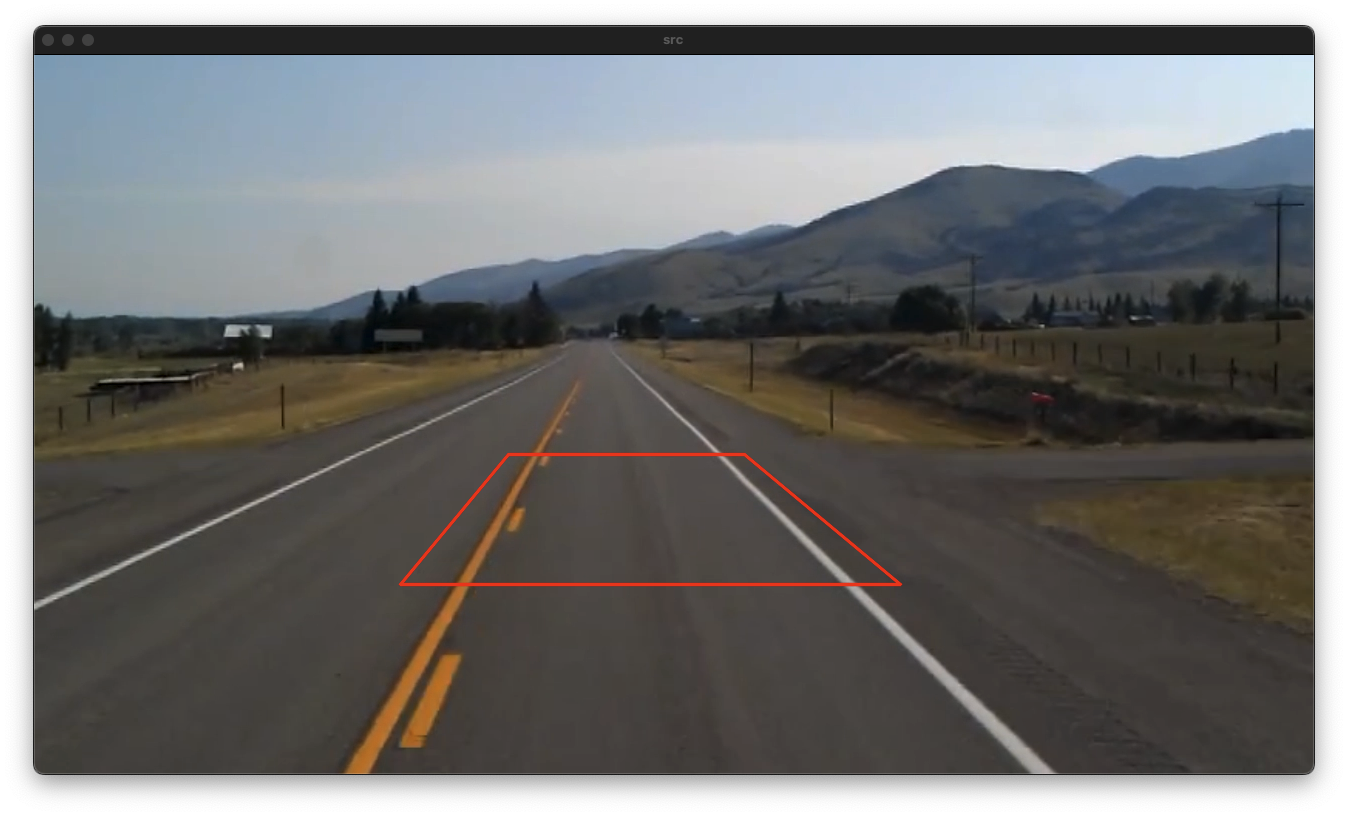
void ex_processing(){
    VideoCapture cap("../data/test_video.mp4");

	if (!cap.isOpened()) {
		cerr << "Video load failed!" << endl;
		return ;
	}

    Mat src;
	while (true) {
		cap >> src;

		if (src.empty())
			break;

		int w = 500, h = 260;

		vector<Point2f> src_pts(4);
		vector<Point2f> dst_pts(4);

		src_pts[0] = Point2f(474, 400);	src_pts[1] = Point2f(710, 400);
		src_pts[2] = Point2f(866, 530); src_pts[3] = Point2f(366, 530);

		dst_pts[0] = Point2f(0, 0);		dst_pts[1] = Point2f(w - 1, 0);
		dst_pts[2] = Point2f(w - 1, h - 1);	dst_pts[3] = Point2f(0, h - 1);

		Mat per_mat = getPerspectiveTransform(src_pts, dst_pts);

		Mat dst;
		warpPerspective(src, dst, per_mat, Size(w, h));

		vector<Point> pts;
		for (auto pt : src_pts) {
			pts.push_back(Point(pt.x, pt.y));
		}
		polylines(src, pts, true, Scalar(0, 0, 255), 2, LINE_AA);
        
        imshow("src", src);
        imshow("dst", dst);

        if (waitKey(1) == 27)
            break;

    }
}

리맵핑(Remapping)

영상의 특정 위치 픽셀을 다른 위치에 재배치하는 일반적인 방법이다.

\[\begin{cases} x & :\ input\\ x` & :\ output \end{cases} \Longrightarrow \begin{cases} x` & =x+200\\ y` & =y+100 \end{cases} \Longrightarrow \begin{cases} x & =x`-200\\ y & =y`-100 \end{cases}\] \[\begin{array}{l} 이동\ 변환:\ \begin{cases} map_{x}( x,y) & =x-200\\ map_{y}( x,y) & =y-100 \end{cases}\\ \\ 상하\ 대칭:\ \begin{cases} map_{x}( x,y) & =x\\ map_{y}( x,y) & =h-1-y \end{cases}\\ \\ 크기\ 변환:\ \begin{cases} map_{x}( x,y) & =x/2\\ map_{y}( x,y) & =y/2 \end{cases} \end{array}\]

void ex_processing(){
    Mat src = imread("../data/lenna.bmp");

	if (src.empty()) {
		cerr << "Image load failed!" << endl;
		return ;
	}

	int w = src.cols;
	int h = src.rows;

	Mat map1 = Mat::zeros(h*2, w*2, CV_32FC1);
	Mat map2 = Mat::zeros(h*2, w*2, CV_32FC1);

	for (int y = 0; y < h*2; y++) {
		for (int x = 0; x < w*2; x++) {
			map1.at<float>(y, x) = (float)x/2;
			map2.at<float>(y, x) = (float)y;
			//map2.at<float>(y, x) = (float)h - 1 - y;
			//map2.at<float>(y, x) = (float)y/2;
		}
	}

	Mat dst;
	remap(src, dst, map1, map2, INTER_LINEAR);
	//remap(src, dst, map1, map2, INTER_LINEAR, BORDER_DEFAULT);

	imshow("src", src);
	imshow("dst", dst);
	waitKey();
}

영상의 기하학적 변환

Table of contents

영상의 기하학적 변환(Geometric transformation)

이동 변환(Translation trnaform)

전단 변환(Shear transform)

크기 변환(Scale transform)

순방향 맵핑(Forward mapping)

역방향 맵핑(Backward mapping)

보간법

resize() 함수를 이용한 사이즈 변환

영상 데이터 축소 시 주의할 점

회전 변환(Rotation transform)

정방향 맵핑(Forward mapping)

역방향 맵핑(Backward mapping)

getRotationMatrix2D() 함수

warpAffine() 함수

Example code

기하학적 변환

어파인 변환(Affine transform)

투시 변환(Perspective tranform)

리맵핑(Remapping)